Artificial Intelligence

The problem

In this first post, we will learn how to solve sudokus using computers in a clever way. I propose a Javascript solution.

Let the hereunder sudoku be the problem to solve.

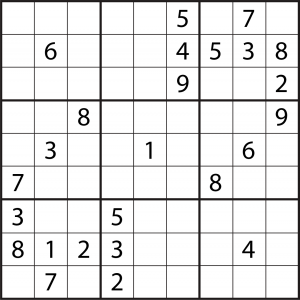
The easiest and stupidest way of solving it would be to bruteforce the grid.
That is, we would try out all possible numbers in every single cell until a solution comes up. Since there are 56 empty cells to fill, the worst case scenario needs 9⁵⁶= 2.74*10⁵³ attempts. Assuming a modern CPU is cappable of 300’000 millions of operations per second (MOPS), this takes up to 2.9*10³⁴ years.

Since our planet will probably be dead by that time, it is wise to find another approach.

Constraint Satisfaction Problem

Given:

$\begin{itemize} \item A set of variables X = \{$x_1$, $x_2$, $\ldots$, $x_n$\} \item A domain for each variable: $D_1$, $D_2$, $\ldots$, $D_n$ \item A set of constraints C = \{$c_1(x_k, x_l, \ldots), c_2, \ldots, c_m$\} \end{itemize}$

We want to find a solution $S = \{x_1 = v_k, x_2 = v_m, \ldots, x_n = v_n\}$ where $v_i$ is the value of the variable $x_i$ .

Note that in our problem we have 56 variables, each has a domain $D = \{1, \ldots, 9\}$ of allowed values and we want to find a solution $S = \{x_1 = v_k, \ldots, x_{56} = v_l\}$ .
If we label every variables starting from the top left corner of the grid, going left to right (row by row) and taking into account only the blank cells, $S$ must then satisfy the following constraints:

no duplicate in the set 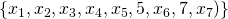$\{x_1, x_2, x_3, x_4, x_5 , 5, x_6, 7, x_7)\}$ – the first line is composed of unique integers
no duplicate in the set 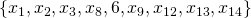$\{x_1, x_2, x_3, x_8, 6, x_9, x_{12}, x_{13}, x_{14}\}$ – the first square is composed of unique integers
etc…

A simple algorithm used to solve CSPs, equivalent to the bruteforce approach described above, is generate and test.
We now take a look at a much more efficient method.

A Depth First Search (DFS) based algorithm

Let the root (the first node) of some oriented graph (tree) $G$ be the empty set, and let each node be an instantiation of the k first variables, e.g. $\{x_1=v_1, \ldots, x_k=v_k\}$ .
The successor of a node is itself plus an instantiation of the $x_{k+1}=v_{k+1}$ so as to respect all the constraints with $x_1, ..., x_k$ .
As shown in the figure below, as soon as a node becomes impossible we discard it (this is called backtracking). This avoids useless exploration of its children.

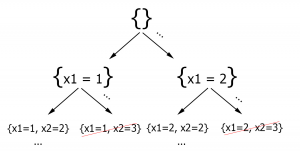
While this new method seems a little faster, its running time is still exponential in the number of variables. We can add two heuristics to complete our algorithm.

Adding the Forward Checking heuristic

The above method doesn’t discard nodes as soon as they become logically impossible.
Indeed, while all the constraints affecting the $k$ first variables might hold, it is likely that some other constraint $c(x_i, \ldots, x_n)$ , $x_i \in \{x_1, \ldots, x_k\}$ is already broken.
As an example of such a case, consider 10 variables. We require the 9 first to have different values, and the 10^th to be strictly greater than all the others. Think of all the paths with 9 instantiated variables with different values that are discarded. What a waste.
In the light of this fact we can optimize our algorithm with the forward checking heuristic.

Add a label (a set) to each variables. Initialize it to the variable’s domain.
At each instantiation, remove from the label of uninstantiated variables all the values that are inconsistent with this instantiation.
As soon as a variable’s label becomes empty, we know that the current instantiation isn’t possible. Go back.

Adding the Dynamic Variables Ordering (DVO) heuristic

At each step of the search, sort the variables by label sizes. Instantiate the variable with the smallest label size.
The gain in speed in intuitive, and we no longer need backtracking.

The algorithm having been fully explained, let’s code!

I give the complete source code on github.
Here is the result:

AutoSudoku

References

CS-330 EPFL
Faltings Boi, and Michael Schumacher. L’intelligence Artificielle Par La Pratique. Lausanne: Presses Polytechniques Et Universitaires Romandes, 2009

Category: Artificial Intelligence

Automatic sudoku solver